A la découverte de java
Dans la série d’article précédente sur l’histoire des langages de programmation, j’ai vu que Java était un des derniers langages de programmation créés.
Cc’est pour ça que j’ai décidé d’utiliser ce langage pour découvrir à quoi ressemble le travail de programmation.
Pour programmer en Java il faut d’abord télécharger un outil de programmation java.
En ce cas j’utilise éclipse. https://www.eclipse.org

Test de l’environnement java.
Une fois qu’on a lancé Eclipse, on crée un nouveau projet.
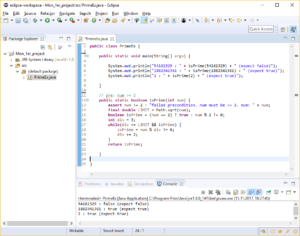
Dans ce projet j’ai recopié le code d’exemple Java que j’avais cité dans l’article sur « l’histoire de la programmation ».
En haut de la fenêtre il y a le code et directement en dessous il y a le résultat de l’exécution du code.
C’est-ce qu’on fait en cliquant sur le petit bouton vert en haut.
Quelques essais de programmes
Pour explorer le langage java, nous avons essayé de réécrire les programmes d’exemples des différents langages exploré dans la série d’articles sur l’histoire de la programmation :
- Exemple « langage machine » : trouver le plus grand nombre
- Exemple « fortran » : le plus grand commun diviseur
- Exemple « cobol » : la multiplication
Dans les articles qui suivent, je vais montrer les programmes que cela donne.
Enfin, je me suis essayé à écrirer un petit programme pour m’aider en mathématiques.
Exemple « langage machine » : trouver le plus grand nombre
De l’original en « langage machine » à sa version java !
public class P02_PlusGrandNombre {
public static void main(String[] args) {
int tableauDeNombres[] = { 12, 56, 42, 87, 23, 14, 3, 97, 18, 23, 52, 35 };
int positionPlusGrandNombre = 0;
for (int posNombreExamin=0; posNombreExamin<tableauDeNombres.length ; posNombreExamin++) {
System.out.println("le nombre " + posNombreExamin +" est "+tableauDeNombres[posNombreExamin]);
if( tableauDeNombres[posNombreExamin] > tableauDeNombres[positionPlusGrandNombre]) {
System.out.println("le nombre " + posNombreExamin +" ("+tableauDeNombres[posNombreExamin]+") est plus grand que le nombre "+positionPlusGrandNombre+" ("+tableauDeNombres[positionPlusGrandNombre]+")");
positionPlusGrandNombre = posNombreExamin;
}
}
System.out.println("le plus grand nombre est le "+positionPlusGrandNombre + " (" + tableauDeNombres[positionPlusGrandNombre] +")" );
}
}
Exemple « fortran » : le plus grand commun diviseur
De l’original en « fortran » à sa version java …
public class P03_PlusGrandCommunDiviseur {
public static void main(String[] args) {
int a = 55;
int b = 33;
int resultat = calculePGCD(a,b);
System.out.println("le PGCD de "+a+" et "+b+" est "+resultat);
}
public static int calculePGCD(int na, int nb) {
int ia = na;
int ib = nb;
while ( ib !=0) {
int itemp = ia;
ia = ib;
ib = itemp % ib;
}
return ia;
}
}
Exemple « cobol » : la multiplication
De l’original en « cobol » à sa version java …
import java.util.Scanner;
public class P04_LaMultiplication {
public static void main(String[] args) {
// ouvre le lecteur
Scanner in = new Scanner(System.in);
// lit les nombres.
System.out.printf("Enter first number: ");
int num1 = in.nextInt();
System.out.printf("Enter second number: ");
int num2 = in.nextInt();
// ça fait le calcul
int result = num1 * num2;
// affiche le resultat
System.out.println("result is = " + result);
// ferme le lecteur
in.close();
}
}
Un premier défi : Utilisation de Java pour résoudre un de mes soucis en mathématique
En mathématique j’oublie souvent d’aller jusqu’au bout dans la réduction des fractions.
Or je sais que quand on divise le numérateur et le dénominateur par leur plus grand diviseur commun on obtient le numérateur et le dénominateur de la fraction réduite.
Dans les programmes d’exemple, j’ai trouvé un programme qui trouve les plus grands diviseurs communs. Alors je vais m’en servir pour calculer les fractions réduites.
Le programme java que voici va m’aider à vérifier les fractions que je dois calculer : on y voit l’appel de l’autre sous-programme :
P03_PlusGrandCommunDiviseur.calculePGCD(numerateur, denominateur) ;
Maintenant plus d’erreur pour réduire mes fractions !
import java.util.Scanner;
public class P05_ReductionFraction {
public static void main(String[] args) {
// ouvre le lecteur
Scanner in = new Scanner(System.in);
// lit les nombres.
System.out.printf("Entre le numérateur: ");
int numerateur = in.nextInt();
System.out.printf("Entre le dénominateur: ");
int denominateur = in.nextInt();
System.out.println("saisie est " + numerateur +"/"+denominateur);
// calcul du pgcd en utilisant le programme d'exemple
int pgcd = P03_PlusGrandCommunDiviseur.calculePGCD(numerateur, denominateur);
//calcul du nouveu numérateur et du nouveau dénominateur
numerateur= numerateur/pgcd;
denominateur= denominateur/pgcd;
// affiche le resultat
System.out.println("resultat est " + numerateur +"/"+denominateur);
// ferme le lecteur
in.close();
}
}
Update 2019 !
Dans le cadre d’un travail personnel sur Raspberry Pi en 2019-2020, j’ai utilisé le langage Python. Pour découvrir Python, j’ai réécrit les mêmes programmes dans ce langage : vous pouvez voir ici à quoi ressemble le résultat !
